Разработка системы KPI

Часто для анализа полученных данных рассчитывают следующие статистические показатели, на основании которых делают выводы.

Средней арифметической величиной называется такое значение признака в расчете на единицу совокупности, при вычислении которого общий объем признака в совокупности сохраняется неизменным.

При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности.

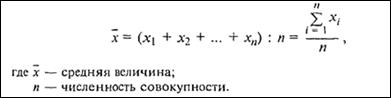
Рисунок 8 – Формула расчета средней арифметической

Медиана — величина варьирующего признака, делящая совокупность на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы.[2]

Рисунок 9 – Формула расчета медианы

Мода - величина признака, которая встречается в изучаемом ряду, в совокупности чаще всего. Отсюда имеем обычно применяемую формулу.

Рисунок 10 – Формула расчета моды

Следующим этапом изучения вариации признака в совокупности является измерение характеристик силы, величины вариации. Простейшим из них может служить размах, или амплитуда вариации, — абсолютная разность между максимальным и минимальным значениями признака из имеющихся в изучаемой совокупности значений. Таким образом, размах вариации вычисляется по формуле

R= Xmax — Xmin

Поскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измерять закономерную силу его вариации во всей совокупности. Предназначенный для данной цели показатель должен учитывать и обобщать все различия значений признака в совокупности без исключения. Поэтому показателем силы вариации выступает не алгебраическая средняя отклонений, а среднее линейное отклонение.

Рисунок 11 – Формула расчета среднего линейного отклонения

Квадрат среднего квадратического отклонения дает величину дисперсии, рассчитывается по формуле.[2]

Рисунок 12 – Формула расчета среднего линейного отклонения

Кластерный анализ

Цель кластерного анализа— классификация объектов на относительно гомогенные (однородные) группы, исходя из рассматриваемого набора переменных. Объекты в группе относительно схожи с точки зрения этих переменных и отличаются от объектов в других группах. Кластерный анализ также называют классификационным анализом. На рисунке13 показана идеальная ситуация кластеризации, когда кластеры четко отделены друг от друга. С другой стороны, на рисунке13 представлена ситуация кластеризации, которая чаще всего встречается на практике - границы некоторых кластеров очерчены нечетко, и отнесение некоторых объектов к конкретному кластеру не очевидно, поскольку многие из них нельзя сгруппировать в тот или иной кластер.

В кластерном анализе нет необходимости в предварительной информации о кластерной принадлежности любого из объектов. Группы, или кластеры, определяют с помощью собранных данных, а не заранее.[8]

Этапы выполнения кластерного анализа представлены на рисунке 14.

1. Формулировка проблемы. Возможно, самая важная часть формулирования проблемы кластеризации — это выбор переменных, на основе которых проводят кластеризацию. Включение даже одной или двух посторонних (не имеющих отношение к группированию) переменных может исказить результаты кластеризации.

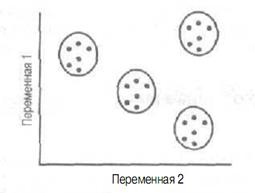
Рисунок 13 – Идеальная и обычная ситуации кластеризации

2. Для того чтобы оценить, насколько они похожи или непохожи, необходимо использовать некую единицу измерения.

Наиболее распространенный метод заключается в том, чтобы в качестве такой меры использовать расстояния между двумя объектами. Существует несколько способов вычисления расстояния между двумя объектами.

Рисунок 14 – Этапы выполнения кластерного анализа[2]

Наиболее часто используемая мера сходства— евклидово расстояние или его квадрат.

Евклидово расстояние - квадратный корень из суммы квадратов разностей в значениях для каждой переменной.

Существуют и другие способы измерения расстояния.

Расстояние городских кварталов или манхэттенское расстояние между двумя объектами — это сумма абсолютных разностей в значениях для каждой переменной.

Расстояние Чебышева между двумя объектами — это максимальная абсолютная разность в значениях для любой переменной.

Использование различных способов измерения расстояния ведет к разным результатам кластеризации. Следовательно, целесообразно использовать различные меры сходства и затем сравнить результаты.

3. Выбрав меру сходства, затем можно выбрать метод кластеризации.

Метод одиночной связи - метод связи, в основе которого лежит минимальное расстояние между объектами, или правило ближайшего соседа.

Метод полной связи - метод связи, в основе которого лежит максимальное расстояние между объектами, или правило дальнего соседа.

Метод средней связи - метод связи, в основе которого лежит среднее значение всех расстояний, измеренных между объектами двух кластеров, при этом в каждую пару входят объекты из разных кластеров.[8]

Широко известным дисперсионным методом, используемым для этой цели, является метод Варда.

Метод Варда - дисперсионный метод, в котором кластеры формируют таким образом, чтобы минимизировать квадраты евклидовых расстояний до кластерных средних.

Центроидный метод - дисперсионный метод иерархической кластеризации, в котором расстояние между двумя кластерами представляет собой расстояние между их центроидами (средними для всех переменных).

К другому типу процедур кластеризации относятся неиерахические методы кластеризации , часто называемые методом к-средних.

Последовательный пороговый метод - неиерархический метод кластеризации, при котором выбирают кластер и все объекты, находящиеся в пределах заданного от центра порогового значения, группируют вместе.

Параллельный пороговый метод - неиерархический метод кластеризации, при котором одновременно определяют несколько кластерных центров. Все объекты, находящиеся в пределах заданного центром порогового значения, группируют вместе.

Метод оптимизирующего распределения - неиерархический метод кластеризации, который позволяет поставить объекты в соответствие другим кластерам (перераспределить объекты), чтобы оптимизировать суммарный критерий.

Два главных недостатка неиерархических методов состоят в том, что число кластеров определяется заранее и выбор кластерных центров происходит независимо. Существует предположение о возможности использования иерархических и неиерархических методов в тандеме. Во-первых, первоначальное решение по кластеризации получают, используя такие иерархические методы, как метод средней связи или метод Варда. Полученное этими методами число кластеров и кластерных центроидов используют в качестве исходных данных в методе оптимизирующего распределения.

 Скачать реферат