Статистика производительности труда
10
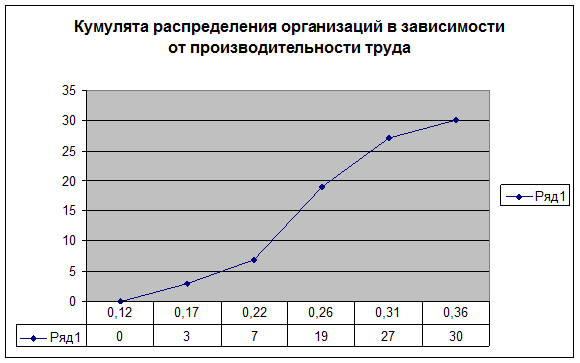
Медиану можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным частотам (табл. 5, графа 5).
Рис. 2. Определение медианы графическим методом
Конкретное значение медианы для интервального ряда рассчитывается по формуле:
, (4)
где хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.
Для расчета медианы необходимо, прежде всего, определить медианный интервал, для чего используются накопленные частоты (или частости) из табл. 5 (графа 5). Так как медиана делит численность ряда пополам, она будет располагаться в том интервале, где накопленная частота впервые равна полусумме всех частот 
или превышает ее (т.е. все предшествующие накопленные частоты меньше этой величины).
В демонстрационном примере медианным интервалом является интервал 0,216 – 0,264 млн руб./чел., так как именно в этом интервале накопленная частота Sj = 19 впервые превышает величину, равную половине численности единиц совокупности (
=
).
Расчет значения медианы по формуле (4):
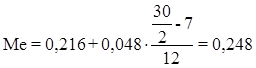млн руб./чел.
Вывод. В рассматриваемой совокупности организаций половина организаций имеют в среднем уровень производительности труда не более 0,248 млн руб./чел., а другая половина – не менее 0,248 млн руб./чел
Расчет характеристик ряда распределения
Для расчета характеристик ряда распределения 
, σ, σ2, Vσ на основе табл. 5 строится вспомогательная таблица 6 (
– середина j-го интервала).
Таблица 6
Расчетная таблица для нахождения характеристик ряда распределения
|
Группы организаций по уровню производительности труда, млн. руб./чел. |
Середина интервала,
|
Число организаций, fj |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0,12 – 0,168 |
0,144 |
3 |
0,432 |
-0,104 |
0,01 |
0,03 |
|
0,168 – 0,216 |
0,192 |
4 |
0,768 |
-0,056 |
0,003 |
0,012 |
|
0,216 – 0,264 |
0,24 |
12 |
2,88 |
-0,008 |
0,000064 |
0,000768 |
|
0,264 – 0,312 |
0,288 |
7 |
2,016 |
0,04 |
0,0016 |
0,0112 |
|
0,312 – 0,36 |
0,336 |
4 |
1,344 |
0,088 |
0,007744 |
0,030976 |
|
Итого |
30 |
7,44 |
- 0,04 |
0,022408 |
0,084944 |
Расчет средней арифметической взвешенной:
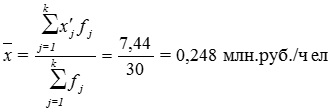
Расчет среднего квадратического отклонения:
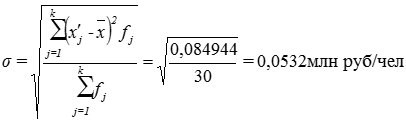
Расчет дисперсии:
σ2=0,05322=0,0028млн.руб/чел.
Расчет коэффициента вариации:
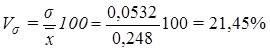
Вывод. Анализ полученных значений показателей и σ говорит о том, что средний выпуск продукции организаций составляет 0,248 млн. руб./чел., отклонение от среднего уровня в ту или иную сторону составляет в среднем 0,0532 млн руб./чел. (или 21,45%), наиболее характерные значения уровня производительности труда находятся в пределах от 0,1948 млн руб./чел. до 0,3012 млн руб./чел. (диапазон 
).
Значение Vσ = 21,45% не превышает 33%, следовательно, вариация уровня производительности труда в исследуемой совокупности организаций незначительна и совокупность по данному признаку качественно однородна. Расхождение между значениями , Мо и Ме незначительно (=0,248 млн руб./чел, Мо=0,245 млн руб./чел., Ме=0,248 млн руб.\чел.), что подтверждает вывод об однородности совокупности организхаций. Таким образом, найденное среднее значение уровня производительности труда (0,248 млн руб./чел.) является типичной, надежной характеристикой исследуемой совокупности организаций.
Скачать реферат