Статистика производительности труда

Вычисление средней арифметической по исходным данным

Для расчета применяется формула средней арифметической простой:

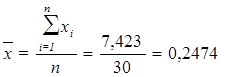(8)

Причина расхождения средних величин, рассчитанных по формулам (8) и (5), заключается в том, что по формуле (8) средняя определяется по фактическим значениям исследуемого признака для всех 30-ти организаций, а по формуле (5) средняя вычисляется для интервального ряда, когда в качестве значений признака берутся середины интервалов и, следовательно, значение средней будет менее точным (за исключением случая равномерного распределения значений признака внутри каждой группы).

Задание 2

По исходным данным табл. 1 с использованием результатов выполнения Задания 1 необходимо выполнить следующее:

1. Установить наличие и характер корреляционной связи между признаками Среднесписочная численность работников и Выпуск продукции, образовав по каждому признаку пять групп с равными интервалами, используя методы:

а) аналитической группировки;

б) корреляционной таблицы.

2. Оценить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.

Сделать выводы по результатам выполнения Задания 2.

Выполнение Задания 2

Целью выполнения данного Задания является выявление наличия корреляционной связи между факторным и результативным признаками, установление направления связи и оценка ее тесноты.

Факторный и результативный признаки либо задаются в условии задания, либо определяются путем проведения предварительного теоретического анализа. Лишь после того, как выяснена экономическая сущность явления и определены факторный и результативный признаки, приступают к проведению корреляционного анализа данных.

По условию Задания 2 факторным является признак Уровень производительности труда (X), результативным – признак Выпуск продукции (Y).

1. Установление наличия и характера связи между признаками Уровень производительности труда и Выпуск продукции методами аналитической группировки и корреляционной таблицы

1а. Применение метода аналитической группировки

При использовании метода аналитической группировки строится интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.

Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х – Уровень производительности труда и результативным признаком Y – Выпуск продукции. Макет аналитической таблицы имеет следующий вид (табл. 7):

Таблица 7

Зависимость суммы прибыли банков от объема кредитных вложений

Групповые средние значения получаем из таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 8.

Таблица 8

Зависимость выпуска продукции организаций от выпуска продукции

 Скачать реферат