Исследование операций

2

x1=6 x1=5,6

x2=1 x2=2

x3=5 x3=4

Z=5993 Z=5991

Вершина	Ограничение	№ ограничения
2	x1 6	7
3	x1 7	7
4	x1 6 x2 1	7 8
5	x1 6 x2 2	7 8

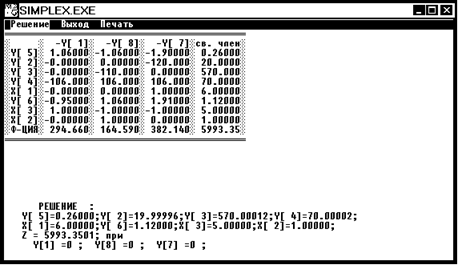
Вывод:

В результате решения я получил, что целочисленное оптимальное решение получается в вершине 4, так как все значения x1=6, x2=1,x3=5 в этой вершине целочисленные и Z5(5991)<Z4(5993), следовательно получено оптимальное решение. Висящая вершина 5 и прозондированные 1,2,3,4.

Плановые задания:

, где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.

Для предприятия 1:

тыс. тонн;

Для предприятия 2:

тыс. тонн;

Для предприятия 3:

тыс. тонн.

Нелинейное программирование.

Задача математического программирования называется нелинейной, если нелинейны ограничения или целевая функция.

Задачи нелинейного программирования бывают выпуклого и невыпуклого программирования, с ограничениями и без ограничений, с квадратичными или сепарабельными целевыми функциями. Задачи нелинейного программирования имеют множество экстремальных точек, и сложность решения заключается в выделении глобального оптимума, а не локального как это делается в большинстве классических методов.

Разделяют задачи безусловной и условной оптимизации. Задачами безусловной оптимизации называются задачи оптимизации функции многих переменных без дополнительных ограничений. Существуют следующие методы безусловной оптимизации: покоординатного спуска, градиентные, сопряженных направлений, метод Ньютона. Задачами условной оптимизации называются задачи о оптимизации целевой функции многих переменных f(x1, …, xn) при условии, что эти переменные удовлетворяют следующим ограничениям:

qi(x1, …, xn) = 0,

или

dj(x1, …, xn)

,

Решение задачи основывается на линейной или квадратичной аппроксимации целевой функции для определения приращений x1, …,xnна каждой итерации.

Существуют также приближенные методы решения нелинейных задач. Это методы основанные на методе кусочно-линейной аппроксимации. Точность нахождения решений зависит от количества интервалов, на которых мы находим решение линейной задачи, максимально приближенной к нелинейной. Такой метод позволяет производить расчеты с помощью симплекс-метода. Обычно в линейных моделях коэффициенты целевой функции постоянны и не зависят от значения переменных. Однако существует ряд задач, где затраты зависят от объема нелинейно. Такие задачи решаются следующим способом: решают задачу ЛП с коэффициентами целевой функции при максимальных значениях переменных. Если в решении мы получили переменные, для которых брались коэффициенты, значит задача решена. В противном случае мы изменяем коэффициенты при целевой функции на коэффициенты при вновь полученных значениях переменных и решаем полученную задачу ЛП. Так мы повторяем до тех пор, пока не будет получено на двух последующих шагах одно и то же решение.

Решение задачи нелинейного программирования.

Метод кусочно – линейной аппроксимации.

В нашей задаче есть такая величина, как коэффициент увеличения затрат при нагрузке, который не использовался нами при решении задачи методами ЛП и ЦЛП. Собственно этот коэффициент и введен для превращения задачи в нелинейную путем нелинейной зависимости между увеличением затрат и загрузкой предприятий.

Составим таблицу:

№ предприятия	Коэффи- Циент затрат %	Количе-ство составов	Коэфф. измене-ния затрат	Затраты на 1т у.е.	Доход	Прибыль На 1т у.е.	Прибыль на 1 состав у.е.
1	2	3	4	5	6	7	8
Њ	100	6,17	1	6	11,64	5,64	676,8
	70 – 100	4.31–6,16	1,4	8,4		3,24	388,8
	50 – 70	3,08–4,31	1,6	9,6		2,04	244,8
	30 – 50	1,85–3,08	1,7	10,2		1,44	172,8
	до 30	до 1,85	1,8	10,8		0,84	100,8
Ќ	100	6,18	1	7	11,175	4,175	459,25
	70 – 100	4,33-6,18	1,2	8,4		2,775	305,25
	50 – 70	3,09-4,33	1,4	9,8		1,375	151,25
	30 – 50	1,85-3,09	1,5	10,5		0,675	74,25
	до 30	до 1,85	1,7	11,9		- 0,725	- 79,75
Ћ	100	5,66	1	8	10,78	2,78	294,66
	70 – 100	3,96-5,66	1,3	10,4		0,38	40,28
	50 – 70	2,83-3,96	1,6	12,8		- 2,02	- 214,12
	30 – 50	1,7 – 2,83	1,7	13,6		- 2,82	- 298,92
	до 30	до 1,7	1,9	15,2		- 4,42	- 458,52