Исследование операций

1) Z1= 8000

8121,6 – 217,55 x2– 382,14 x3= 8000

-217,55 x2– 382,14 x3= 8000 – 8121,6

217,55 x2+ 382,14 x3=121,6

2) Z2= 9000

-217,55 x2– 382,14 x3= 9000 – 8121,6

217,55 x2+ 382,14 x3= – 878,4

Мы получили, что график функции Z2расположен ниже чем график функции Z1. Однако Z2> Z1(9000 > 8000). Следовательно своего максимального значения целевая функция достигает в самой нижней точке области относительно целевой функции (в той точке, через которую график целевой функции будет проходить первым при уменьшении целевой функции). Обозначим эту точку на графике A. Координаты точки A (0,95;4,89). x2= 0,95; x3= 4,89, что соответствует решению с помощью симплекс – метода.

2. Задача ЦЛП.

Максимального значения целевая функция задачи ЦЛП достигает при x2= 1, x3= 5. На графике решение задачи ЦЛП – точка B с координатами (1;5).

3. Задача нелинейного программирования.

x2= 0,17, x3= 5,66. На графике точка C с координатами (0,17;5,66).

4. Задача ДП.

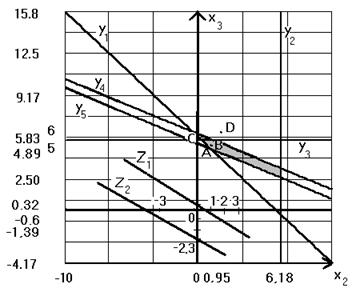x2= 2, x3= 6. На графике точка D с координатами (2;6).

Трудоемкость и эффективность решения модели различными методами.

О проекте.

Проект выполнен студентом второго курса факультета РПМ Московского государственного горного университета Солодовниковым Дмитрием.

Использованная литература:

· Резниченко С. С., Ашихмин А.А. Математические методы и моделирование в горной промышленности. – М.: Издательство Московского горного университета, 1997, 404 c.

 Скачать реферат