Исследование операций

Где доход (Д) рассчитывается по формуле:

, где

Ц – цена готовой продукции, Е – извлечение, a - содержание полезного компонента.

Прибыль (П) рассчитывается по формуле:

П = Д – З , где Д – доход, З – затраты.

Затраты (З) рассчитываются по формуле:

, где С – затраты на добычу, транспортировку и переработку,

коэффициент изменения затрат.

1. Пусть x1, x2, x3принимают свои максимальные значения, тогда

Z1= 676,8x1+ 459,25x2+ 294,66x3

MAX

Ограничения:

x1+ x2+ x3=12 – по количеству составов;

x1

6,17 - максимальный объем добычи руды с предприятия 1;

x2

6,18 - максимальный объем добычи руды с предприятия 2;

x3

5,66 - максимальный объем добычи руды с предприятия 3;

0,96x1+ 0,11x2– 0,95x3

0 – по максимально допустимому содержанию полезного компонента в руде;

-0,84x1+ 1,06x3

0 – по минимально допустимому содержанию

полезного компонента в руде.

Решение 1.

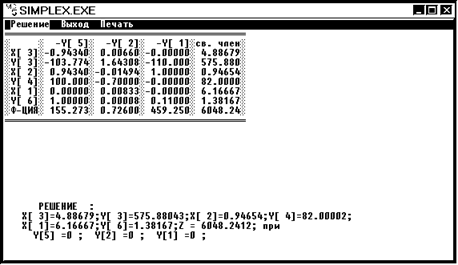
x1 = 6,17 x2 = 0,95 x3=4,88 Z1= 6048,24

2. Так как x1=6,17 – максимально возможный, то коэффициент при x1в

целевой функции Z2будет равен 676, 8.

Так как x2=0,95; x2< 1,87, то коэффициент при x2в целевой функции Z2будет равнятся -79,75.

Так как x3=4,88; 3,96 < 4,88 <5,66, следовательно x3попадает в интервал 3,96 – 5,66, следовательно коэффициент при x3в целевой функции Z2 будет равен 40,28.

Следовательно Z2= 676,8x1– 79,75x2+ 40,28x3

Решение 2.

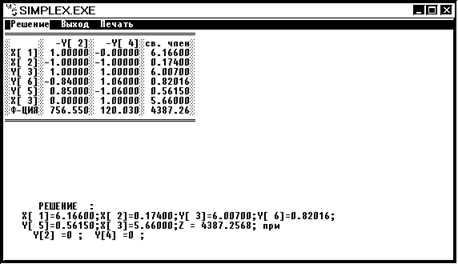
x1 = 6,17 x2 = 0,17 x3= 5,66 Z2= 4387,26

3. Так как x1=6,17 – максимально возможный, то коэффициент при x1в

целевой функции Z3будет равен 676, 8.

Так как x2=0,17; x2< 1,87, то коэффициент при x2в целевой функции Z3будет равнятся -79,75.

Так как x3=5,66 – максимально возможный, то коэффициент при x3в

целевой функции Z3будет равен 294,68.

Следовательно Z3= 676,8x1– 79,75x2+ 294,68x3

Решение 3.

x1= 6,166 x2= 0,17 x3= 5,66 Z3= 5827,16

Вывод:

Так как на третьем шаге мы получили значения переменных равных значениям переменных на втором шаге, то мы получили искомое решение задачи нелинейного программирования. Третий шаг, за счет того, что значения коэффициента при x3были увеличены с 40,28 до 294,68, улучшил целевую функцию Z3на 5827,16 – 4387,26 = 1439,9 у.е.

Плановые задания предприятиям.

, где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.

Для предприятия 1:

тыс. тонн;

Для предприятия 2:

тыс. тонн;

Для предприятия 3:

тыс. тонн.

Аппроксимация кривой зависимости затрат от количества составов. Примеры графиков для предприятий 1 и 2.

Динамическое программирование. (ДП)

Динамическими называются задачи экономики, организации и управления, в которых необходимо распределять ресурсы на каждом этапе какого – либо промежутка (времени). Формулировка задачи ДП:

Имеется некая система S, находящаяся в первоначальном состоянии S. Данная система имеет какие – либо параметры. При переходе системы из одной точки в другую необходимо в каждый момент времени выбирать направление дальнейшего движения из нескольких допустимых направлений при условии, что каждому направлению соответствует своя эффективность (параметры системы изменяются по разному), и необходимо таким образом спланировать маршрут из начальной точки в конечную, чтобы критерий эффективности достигал экстремального значения.

Иными словами из множества допустимых управлений U=(U1, U2, …, Un) необходимо найти оптимальное, при котором система переходит из своего начального состояния в конечное таким образом, что критерий оптимальности W достигает своего максимума.

Динамическое программирование представляет собой метод оптимизации многошаговых процессов по шагам. Локальный оптимум на каждом шаге должен рассчитываться не как оптимальный на данном этапе, а как дающий максимальное значение критерия оптимальности в конце движения. Несоблюдение этого правила приводит к серьезным ошибкам, поэтому при решении задач ДП двигаются обычно из конца пути в начало, рассчитывая затраты при движении в каждом направлении, а затем из начала в конец, находя локальный оптимум из рассчитанных затрат на каждом шаге. Таким образом получаем максимальное значение критерия оптимальности.

В основе расчетов методом динамического программирования лежит принцип Беллмана. Он звучит:

оптимальное управление обладает тем свойством, что какавы бы ни были достигнутые состояния и решения до данного момента, последующее решение должно составлять оптимальное поведение относительно состояния, достигнутого на данный момент.

Решение задачи динамического программирования.

Распределение ресурсов предприятиям.