Обзор методов графического представления моделей в экономике и управлении

Далее, устанавливаем на плане окна и двери. Из набора элементов Структурные элементы, выбираем и перетаскиваем на страницу документа соответствующие фигуры и устанавливаем их в место их расположения. Они автоматически займут свое положение в проеме стены. Для изменения размера дверей и окон, пользуемся уже знакомым нам инструментом Размер и положение. Для изменения направления открытия дверей и окон выделите соответствующую фигуру или фигуры. Щелкните их правой кнопкой мыши, а затем в контекстном меню выберите нужную команду направления открытия.

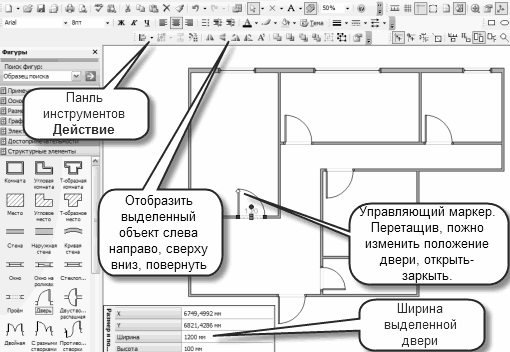
При необходимости, можно добавить к стенам размерные линии. Для этого щелкните правой кнопкой мыши фигуру стены, а затем в контекстном меню выберите команду Добавить размер. Измените, положение размерных линий и размерного текста, перетащив управляющий маркер. Для добавления дополнительных размеров на плане, в меню Файл последовательно выберите команды Фигуры, Дополнительные решения Visio, Размеры. Выбираем и перетаскиваем на страницу документа соответствующие фигуры размеров.

Для нашего проекта нанесем на плане квартиры назначение помещений, и их размеры. Для этого в меню Вставка выберите команду Надпись (Можно также нажать кнопку Текст на панели инструментов Стандартная. Если кнопка Текст не отображается, то щелкните стрелку рядом с кнопкой Блок текста и выберите пункт Текст).

Щелкните страницу в любом месте или, нажав и удерживая кнопку мыши, перемещайте указатель, пока рамка текстового блока не достигнет нужного размера. Введите текст. Повторите для каждого из блоков текста, которые требуется добавить. Полученные текстовые блоки в дальнейшем можно переместить в любое место. Двойной щелчок на текстовом блоке позволит изменить введенный текст.

Сохраняем полученный документ. В дальнейшем он понадобится для составления осветительной и розеточной сети

Основные понятия теории графов

Граф – система, которая интуитивно может быть рассмотрена как множество кружков и множество соединяющих их линий (рис. 1).

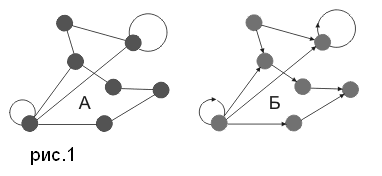
Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами. Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным (рис. 1, А); граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным (рис. 1, Б).

Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Будем обозначать вполне несвязный граф с п вершинами через Nn; N4 показан на рис. 1. Заметим, что у вполне несвязного графа все вершины изолированы. Вполне несвязные графы не представляют особого интереса.

Простой граф, в котором любые две вершины смежны, называется полным графом. Полный граф с n вершинами обычно обозначается через . Графы и изображены на рис. 2 и 3. имеет ровно n (n – 1)/2 ребер.

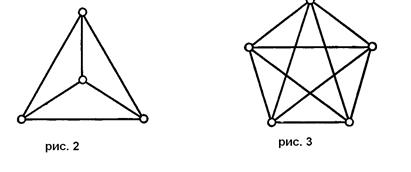
Регулярные графы. Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна r, то граф называется регулярным степени r. Регулярные графы степени 3, называемые также кубическими (или трехвалентными) графами (см., например, рис. 2 и 4). Другим известным примером кубического графа является так называемый граф Петерсена, показанный на рис. 5. Отметим, что каждый вполне несвязный граф является регулярным степени 0, а каждый полный граф Кn – регулярным степени n – 1.

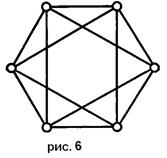
Среди регулярных графов особенно интересны так называемые Платоновы графы – графы образованные вершинами и ребрами пяти правильных многогранников – платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра. Граф соответствует тетраэдру (рис. 2); графы, соответствующие кубу и октаэдру, показаны на рис. 5 и 6;

Двудольные графы. Допустим, что множество вершин графа можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-либо вершиной из V2 (рис. 7);

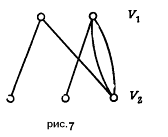
тогда G называется двудольным графом. Такие графы иногда обозначают G(V1,V2), если хотят выделить два указанных подмножества. Двудольный граф можно определить и по-другому – в терминах раскраски его вершин двумя цветами, скажем красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы любое ребро имело один конец красный, а другой – синий. Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая вершина из V1 соединена с каждой вершиной из V2; если же это так и если при этом граф G простой, то он называется полным двудольным графом и обычно обозначается где m, n – число вершин соответственно в V1 и V2. Например, на рис. 8 изображен

граф K4,3. Заметим, что граф имеет ровно m + n вершин и mn ребер. Полный двудольный граф вида называется звездным графом; на рис. 9 изображен звездный граф .

Связные графы. Граф связный, если его нельзя представить в виде объединения двух графов, и несвязный в противном случае. Очевидно, что всякий несвязный граф G можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой (связности) графа G. (На рис. 10 изображен граф с тремя компонентами.) Доказательство некоторых утверждений для произвольных графов часто бывает удобно сначала провести для связных графов, а затем применить их к каждой компоненте в отдельности.

Циклические графы и колеса. Связный регулярный граф степени 2 называется циклическим графом (или циклом); циклический граф. с п вершинами обозначается через Сn. Соединение графов и (п ≥ 3) называется колесом с п вершинами и обозначается Wn. На рис. 11 изображены С6 и W6; граф W4 уже появлялся на рис. 2.

 Скачать реферат