Распределенная автоматизированная система управления

Так как максимальное напряжение на входе АЦП , то коэффициент передачи усилителя напряжения (УН) составит:

Передаточная функция сервопривода имеет вид:

,

где определяется как:

,

- коэффициент усиления датчика положения:

,

Подставляя (2.16) в (2.15), получим

постоянную времени сервопривода найдём следующим образом:

,

- номинальное время полного хода выходного вала, с, следовательно

Подставляя (2.17) и (2.18) в (2.14) получим:

,

Коэффициент передачи регулирующего органа равен:

;

Так как расход выходного потока равен:

,

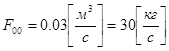то коэффициент пересчёта равен:

,

Согласно формулам (2.13) и (2.19) и с учетом того, что :

Моделирование производилось в среде SIMULINK 4 пакета прикладных программ MATLAB версии 6.1.0.450 Release 12. К моделированию была представлена схема, изображенная на рис. 3.8.

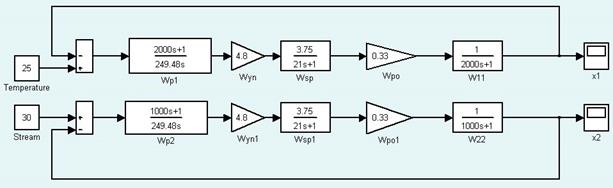
Рис. 2.7. Схема для исследования работы контуров без учета взаимного влияния.

Результаты моделирования отдельных контуров представлены на рис. 2.8, 2.9.

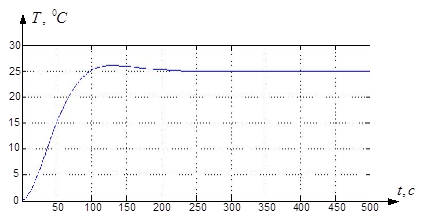
Рис. 2.8. Переходной процесс в контуре стабилизации температуры без учета взаимного влияния контуров.

Рис. 2.9. Переходной процесс в контуре стабилизации расхода выходного потока без учета взаимного влияния контуров.

Исследование взаимного влияния контуров

Так как контура исследуемой системы находятся во взаимном влиянии, то при учете этого обстоятельства структурная схема принимает следующий вид:

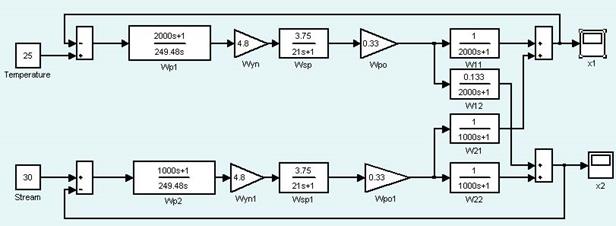
Рис. 2.10. Схема для исследования взаимного влияния контуров.

В этом случае результаты моделирования имеют вид, представленный на рис. 2.12, 2.13.

Рис. 2.11. Переходной процесс в контуре стабилизации температуры с учетом взаимного влияния контуров.

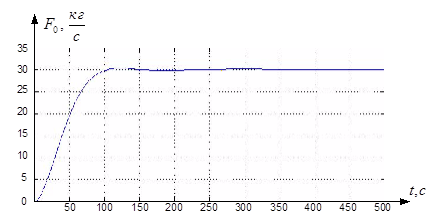
Рис. 2.12. Переходной процесс в контуре стабилизации температуры с учетом взаимного влияния контуров.

По переходным характеристикам системы представленной на рис. 2.11 можно сделать вывод о том, что учет взаимного влияния контуров приводит к резкому увеличению перерегулирования в контуре стабилизации температуры выходного потока.

Для компенсации взаимного влияния контуров используется корректирующие перекрёстные связи Wрк1 и Wрк2 между каналами регулирования, которые компенсируют перекрёстные связи объекта управления рис. 2.4 [5].

Для определения передаточных функций компенсационных регуляторов Wрк1 и Wрк2 , воспользуемся формулой Мейсона. Запишем передаточную функцию замкнутой системы для канала 1-2 , из точки в точку [1].

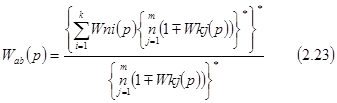
где – передаточная функция i-го прямого пути из точки в точку ;

k – число прямых путей из точки в точку ;

– передаточная функция j-го замкнутого контура;

m – число замкнутых контуров.

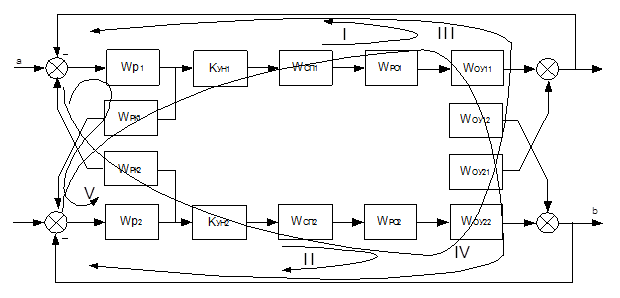
Рис. 2.13. Структурная схема управления смесительным устройством.

Рассматриваемая система имеет два прямых пути из точки в точку :

и пять замкнутых контуров:

Подставляя (2.24)-(2.30) в (2.23) и решая полученное уравнение относительно , получим:

Так как , то из (2.31) имеем:

Аналогичным образом находится передаточная функция .

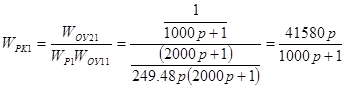
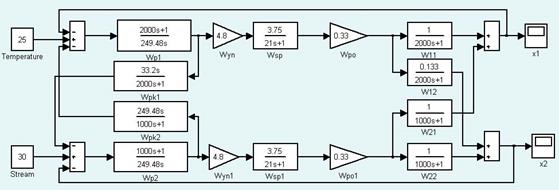
Рис. 2.14. Схема для исследования компенсации взаимного влияния контуров.

Рис. 2.15. Переходной процесс в контуре стабилизации температуры с компенсацией взаимного влияния контуров.

 Скачать реферат