Анализ основных этапов построения и решения математических моделей оптимизации организационных структур в системе менеджмента качества

Находим координаты точек:

A (х1 = 10; х2 = 0);

B (х1 = 10; х2 = 6);

C (х1 = 1,39; х2 = 6);

D(х1 = 5,5;х2 = 0);

Если заранее зафиксировать значение целевой функции , то соответствующие ему точки будут лежать на некоторой прямой. При изменении величины Z эта прямая подвергается параллельному переносу. Рассмотрим прямые, соответствующие различным значениям Z, имеющие с допустимой областью хотя бы одну общую точку. Начальное значение Z положим равным 257.

1 шаг:

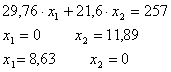
2 шаг:

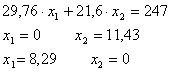
При приближении прямой к началу координат значение Z уменьшается. Если прямая имеет хотя бы одну общую точку с допустимой областью ABC, ее можно смещать в направлении начала координат. Ясно, что для прямой, проходящей через точку С с координатами х1 = 1,39; х2 = 6, дальнейшее движение не возможно. Точка С представляет собой наилучшую допустимую точку, соответствующую наименьшему значению. Следовательно, х1 = 1,39; х2 = 6 – оптимальное решение и Z = 170,9 ДЕ – оптимальное значение рассматриваемой задачи.

Дробное значение х1 = 1,39 соответствует использованию одного из контролеров разряда 1 в течение неполного рабочего дня. При недопустимости неполной загрузки контролеров дробное значение обычно округляют, получая приближенное оптимальное целочисленное решение

х1 = 1; х2 = 6.

Решение х1 = 1; х2 =6 – единственная допустимая точка с минимальным значением Z. Другими словами, значения Z, соответствующие другим допустимым решениям, больше 170,9. В силу этого решение

х1 =1,39; х2 = 6 называется единственным оптимальным значением.

На рис.1 представлено графическое решение задачи.

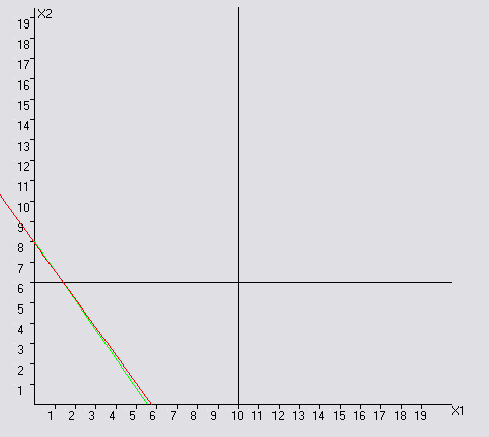
Рис. 1 Графическое решение задачи

3.2 Решение задачи оптимизации методом математического моделирования

Для решения задачи оптимизации используем метод равномерного поиска. Этот метод основан на последовательном переборе значений оптимизируемых параметров с определенным шагом и проверке в них функциональных ограничений. Формируется набор точек из допустимой области решений. Оптимальное решение задачи соответствует точке с минимальным значением целевой функции. На рис.2 приведена блок – схема метода равномерного поиска.

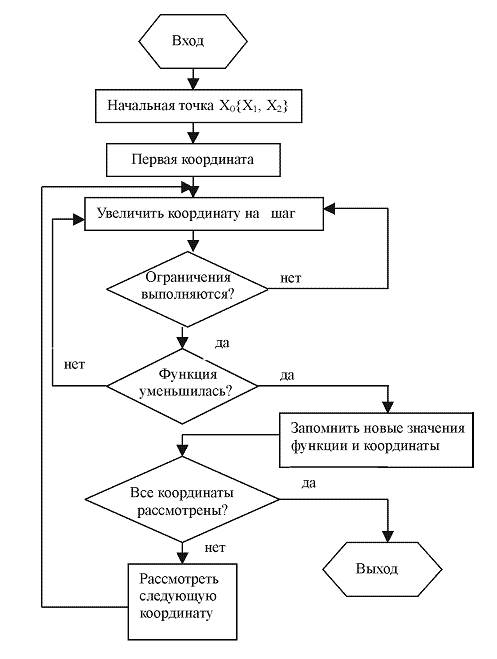
Рис. 2 Блок-схема метода равномерного поиска

По программе, реализующей метод равномерного поиска, рассчитываются значения оптимальных параметров х1 и х2.

4. Реализация на ЭВМ

4.1 Код программы

Public x1, x2, x3, x4 As Double

Public x5, x6, z, d As Integer

Private Sub Command1_Click()

Command2.Enabled = True

Picture1.Cls

Picture2.Cls

x1 = Val(Text4) + Val(Text6) * Val(Text2) * (100 - Val(Text9)) / 100

x2 = Val(Text5) + Val(Text6) * Val(Text3) * (100 - Val(Text10)) / 100

x4 = Val(Text1) / (Val(Text2) * 8)

x3 = Val(Text1) / (Val(Text3) * 8)

Picture2.Print "Z = " & x1 * 8 & "*X1" & "+" & x2 * 8 & "*X2"

Picture2.Print Val(Text2) & "X1+" & Val(Text3) & "X2>=" & Val(Text1) / 8

Picture1.Line (40, 400)-(40, 10)

Picture1.PSet (44, 10), RGB(255, 255, 255)

Picture1.Print "X2"

Picture1.Line (40, 400)-(450, 400)

Picture1.Print "X1"

For i = 1 To 19

Picture1.Line (40, 400 - i * 20)-(35, 400 - i * 20)

Picture1.PSet (20, 400 - i * 20), RGB(255, 255, 255)

Picture1.Print i

Picture1.Line (40 + i * 20, 400)-(40 + i * 20, 405)

Picture1.PSet (30 + i * 20, 405), RGB(255, 255, 255)

Picture1.Print i

Picture1.Line (40 + Val(Text7) * 20, 10)-(40 + Val(Text7) * 20, 400)

Picture1.Line (40, 400 - Val(Text8) * 20)-(450, 400 - Val(Text8) * 20)

Picture1.Line (40, 400 - x3 * 20)-(40 + x4 * 20, 400), RGB(0, 255, 0)

Next

End Sub

Private Sub Command2_Click()

Picture3.Cls

x6 = (Val(Text1) - Val(Text2) * 8 * Val(Text7)) / (Val(Text3) * 8)

x5 = (Val(Text1) - Val(Text3) * 8 * Val(Text8)) / (Val(Text2) * 8)

z = Val(Text7) * x1 * 8 + Val(Text8) * x2 * 8

If Val(Text2) / Val(Text3) > x1 / x2 Then

d = x5 * 8 * x1 + Val(Text8) * 8 * x2

Picture3.Print d

Picture1.Line (40 + (z / (8 * x1) * 20) - (Val(Text7) - x5) * 20, 400)-(40 - (Val(Text7) - x5) * 20, 400 - (z / (8 * x2) * 20)), RGB(255, 0, 0)

Else

Picture1.Line (40 + (z / (8 * x1) * 20), 400 + (Val(Text8) - x6) * 20)-(40, 400 - (z / (8 * x2) * 20) + (Val(Text8) - x6) * 20), RGB(255, 0, 0)

d = Val(Text7) * 8 * x1 + x6 * 8 * x2

Picture3.Print d

End If

End Sub

Private Sub Command3_Click()

End

End Sub

Private Sub Command4_Click()

Form2.Show

End Sub

Private Sub Form_Load()

Command2.Enabled = False

End Sub

Программа написана на языке программирования Visual Basic v. 6.0

4.2 Внешний вид и результаты вычисления программы

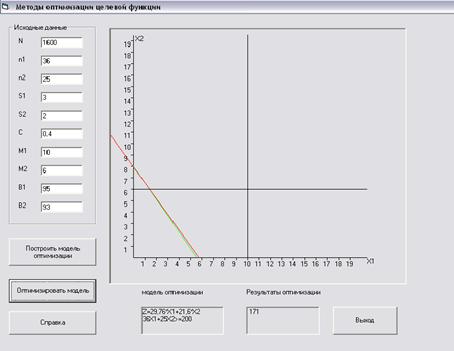
Рис. 3 Результаты вычисления программы

На рис.3 показан интерфейс разработанной программы и результаты её вычисления.

оптимизация математическое моделирование менеджмент

Анализ полученных результатов

Сравнив значения оптимальных параметров найденных графическим методом и методом математического моделирования можно прийти к выводу, что они совпадают и погрешность расхождения результатов не превышает 0,5%.

Результаты проведенных исследований занесены в бланк отчета:

Исходные данные:

Условные обозначения величин:

N - норма выработки изделий группой контролеров ОТК за 8-ми часовой рабочий день;

n1 - Количество изделий, проверяемых контролером 1 разряда в час;

 Скачать реферат