Количественная оценка конкурентных позиций фирмы на рынке

Уже сам по себе размер крупнейших фирм может служить характеристикой концентрации на рынке. Именно этот критерий лежит в основе определения монопольной ситуации в России (свидетельством монополизма служит контроль не менее 35% рынка), в Великобритании (соответственно не менее 25% рынка).

Показатели концентрации

Индекс концентрации измеряется как сумма рыночных долей фирм, действующих на рынке:

, где i=1,2: k

где Yi - размер фирмы (например рыночная доля);

k - количество фирм, для которых рассчитывается показатель.

Индекс концентрации измеряет сумму долей k крупнейших фирм на рынке. Для одного и того же числа фирм, чем больше индекс концентрации, тем дальше рынок от идеала совершенной конкуренции.

Однако, знания этого показателя недостаточно для характеристики рынка, так как он не говорит о том, каков размер фирм, которые не попали в выборку k, а также об относительной величине этой выборки. Это вызывает возможность неточности при его использовании. При изменении числа фирм, попавших в выборку меняются показатели индекса концентрации.

Индекс Херфиндаля-Хиршмана (ННI) определяется как сумма квадратов долей всех фирм, действующих на рынке:

, где i = 1, 2 ::n.

HHI принимает значения от 0 ( в случае идеальной конкуренции, когда на рынке бесконечно много продавцов, каждый из которых контролирует ничтожную долю рынка) до 1 (когда на рынке действует только одна фирма, производящая 10% выпуска). При расчете рыночной доли в % HHI будет принимать значения от 0 до 10 000. Чем больше значение индекса, тем выше концентрация продавцов на рынке.

Основное преимущество индекса - способность чутко реагировать на перераспределение долей между фирмами, действующими на рынке. Он представляет сопоставимую информацию о возможности фирм влиять на рынок в условиях разных рыночных структур.

Значение HHI прямо связано с показателем дисперсии долей фирм на рынке:

,

где

- показатель дисперсии долей фирм на рынке.

Дисперсия долей фирм на рынке позволяет разграничить влияние на HHI числа фирм и распределения рынка между ними. Измеряет степень неравенства размеров фирм, действующих на рынке. Она определяется по известной формуле:

,

где

- средняя доля фирмы на рынке = 1/n, причем n - число фирм на рынке.

Если фирмы на рынке контролируют одинаковую долю, показатель дисперсии равен нулю, и значение HHI обратно пропорционально числу фирм на рынке. При неизменном числе фирм на рынке, чем больше различаются их доли, тем выше значение индекса.

Часто этот показатель (особенно на Западе) заменяется показателем дисперсии логарифмов рыночных долей:

Оба показателя имеют одинаковый экономический смысл, а отличаются лишь размерностью и значениями.

Чем больше неравномерность распределения долей, тем более концентрированным при прочих равных условиях является рынок. Дисперсия применяется в качестве вспомогательного инструмента анализа, так как не дает характеристику относительного размера фирм, причем скорее для оценки неравенства в размерах фирм, чем уровня концентрации.

Индекс энтропии показывает среднюю долю фирм, действующих на рынке, взвешенную по натуральному логарифму обратной ей величины:

,

где i=1,2: n.

Индекс энтропии представляет собой показатель, обратный концентрации: чем выше его значение, тем ниже концентрация продавцов на рынке. Энтропия измеряет неупорядоченность распределения долей между фирмами рынка: чем выше показатель энтропии, тем ниже возможности продавцов влиять на рыночную цену. Для сравнения показателей энтропии часто используют относительный показатель энтропии:

Индекс Джини представляет собой статистический показатель, основывающийся на кривой Лоренца. Кривая Лоренца, отражающая неравномерность распределения какого-либо признака, для случая концентрации продавцов на рынке показывает взаимосвязь между процентом фирм на рынке и долей рынка, подсчитанной нарастающим итогом, от мельчайших до крупнейших фирм. Пример построения кривой Лоренца для рынка А показана на рис.1. Характеристика рынка А приведена в табл.1.

Таблица 1

Характеристика рынка А

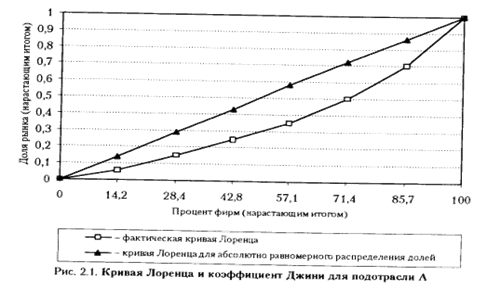Рис.1 Кривая Лоренца и коэффициент Джини для рынка А.

Индекс Джини представляет собой отношение площади, ограниченной фактической кривой Лоренца и кривой Лоренца для абсолютно равномерного распределения к площади треугольника, ограниченного кривой Лоренца для абсолютного равномерного распределения долей и осями абсцисс и ординат.

Расчет индекса Джини показывает, что в данном случае он составляет приблизительно 0,18. Чем выше индекс Джини, тем выше неравномерность распределения рыночных долей между продавцами, и следовательно, при прочих равных условиях выше концентрация на рынке.

При использовании индекса Джини для характеристики концентрации продавцов следует учитывать два важных момента. Первый связан с концептуальным недостатком индекса. Он характеризует, как и показатель дисперсии логарифмов долей, уровень неравномерности распределения рыночных долей. Следовательно, для гипотетического конкурентного рынка, где 10 000 фирм делят между собой рынок на 10 000 равных долей и для рынка дуополии, где две фирмы делят рынок пополам, показатель Джини будет одним и тем же. Второй момент связан со сложностью подсчета индекса Джини: для его определения необходимо знание долей всех фирм в отрасли, в том числе и мельчайших.

Барьеры входа на рынок и выхода с рынка

 Скачать реферат