Рабочее место экспериментатора и его организация
2
Составить содержание пояснительной записки к курсовой работе, выполнить фрагмент раздела (с заголовками) и составить с пояснениями формулу с данными, приведенными в методичке
Введение
1 Определение себестоимости и цены изделия
1.1 Определение затрат на материалы и комплектующие изделия
1.2 Расчет основной заработной платы производственных рабочих
1.3 Расчет других затрат и составление калькуляции
2 Оценка производственной технологичности изделия
3 Технико-экономические расчеты по определению ресурсов
Выводы
Перечень ссылок
Приложение А. Баланс предприятия
Приложение Б. Отчёт о финансовых результатах
Расчет прямой заработной платы основных производственных работников рассчитывается по формуле
, грн. (1.1)
где Зп – прямая заработная плата, грн.;
Стi – сумма прибыли среднечасовой тарифной ставки i-го разряда, грн.;
ti – трудоемкость i-го вида робот, час.
2.2 Рассчитать значения и отобразить на графике функцию y = f(x) по данным приведенным ниже. Где а = 0,7; b = 3,6. Подставляя значения в формулу получаем следующие значения. По полученным значениям строим график.
Таблица 2.1
|
№ эксперимента |
x |
|
|
1 |
1,5 |
10,24 |
|
2 |
2,4 |
24,16 |
|
3 |
1,8 |
14,24 |
|
4 |
1,6 |
11,50 |
|
5 |
2,5 |
26,07 |
|
6 |
3,2 |
41,44 |
|
7 |
2,8 |
32,22 |
|
8 |
2,6 |
28,05 |
|
9 |
4,2 |
69,50 |
|
10 |
4,6 |
82,75 |
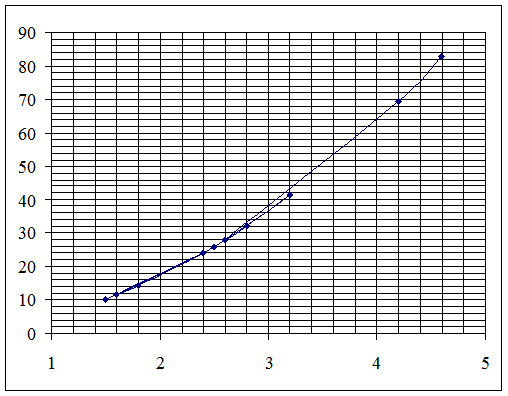
Рисунок 2.1
Используя отдельные элементы вероятностно-статистического метода исследований рассчитать для выборочной совокупности вероятность появления события, среднеарифметическое значение события, математическое ожидание распределения, дисперсию, среднеквадратичное отклонение и коэффициент вариации по данным приведенным в таблице 2.2.
Таблица 2.2
|
№ события |
Значение события |
Количество случаев которые привели к появлению события |
Общее число событий |
|
x |
N(x) |
N | |
|
1 |
5 |
23 |
150 |
|
2 |
3 |
0 | |
|
3 |
4 |
27 | |
|
4 |
2 |
22 | |
|
5 |
2 |
28 | |
|
6 |
4 |
10 | |
|
7 |
4 |
34 | |
|
8 |
5 |
6 |
Рассчитаем вероятность появления события по формуле для каждого события и результат поместим в таблице 2.3
, (2.1)
где N(x) – количество случаев которые привели к появлению события;
N – общее число событий.
Среднеарифметическое значение события
, (2.2)
где n – количество значений событий.
Математическое ожидание распределения, результат расчета в таблице 2.3.
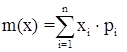. (2.3)
Дисперсия находится по формуле
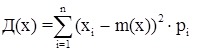. (2.4)
Среднеквадратичное отклонение характеризует теоретическую кривую распределения и рассчитывается по формуле
. (2.5)
Коэффициент вариации находится в относительных единицах по формуле
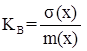. (2.6)
Таблица 2.3
|
x |
N(x) |
N |
p |
m(x) |
x-m(x) |
x-m(x)^2 |
Д(х) |
σ(х) |
Кв |
|
5 |
23 |
150 |
0,15 |
4,45 |
0,55 |
0,31 |
8,15 |
2,86 |
0,64 |
|
3 |
0 |
150 |
0 |
0 |
3 |
9 |
0 |
0 |
дел. на 0 |
|
4 |
27 |
150 |
0,18 |
5,22 |
-1,22 |
1,49 |
9,57 |
3,09 |
0,59 |
|
2 |
22 |
150 |
0,15 |
4,25 |
-2,25 |
5,08 |
7,80 |
2,79 |
0,66 |
|
2 |
28 |
150 |
0,19 |
5,41 |
-3,41 |
11,65 |
9,92 |
3,15 |
0,58 |
|
4 |
10 |
150 |
0,07 |
1,93 |
2,07 |
4,27 |
3,54 |
1,88 |
0,97 |
|
4 |
34 |
150 |
0,23 |
6,57 |
-2,57 |
6,62 |
12,05 |
3,47 |
0,53 |
|
5 |
6 |
150 |
0,04 |
1,16 |
3,84 |
14,75 |
2,13 |
1,46 |
1,26 |
Скачать реферат