Анализ результатов процессного управления маркетингом предприятия сферы услуг

Таблица 3.5

Динамика изменения прибыли от продаж по данным Формы № 2 “Отчет о прибылях и убытках

Верификация имитационной модели состоит в подгонке ее параметров таким образом, чтобы данные моделирования от прошлого к настоящему (например, с 2000 по 2004 годы) совпадали с изменением соответствующих параметров реальной системы, динамику развития которой мы собираемся исследовать.

В нашем случае этот период от 01.01.2002 по 01.07.2004. В качестве базовой переменной на основании которой происходила подгонка модели были выбраны следующие переменные:

прибыль;

выручка (нетто) от реализации услуг;

себестоимость реализации услуг.

Результаты расчетов по подгонке параметров модели , представлены на Рис.3.10 ¸ 3.12.

Как видно из анализа рисунка 3.10 относительная погрешность (в %) к абсолютному значению начинает возрастать, но остается в 5% допуске при появлении нелинейности в исходной функции.

Рис. 10. Результаты подгонки параметров модели по переменной выручка.

Как видно из анализа Рис.3.11 тенденция, отмеченная нами в предыдущем рисунке, сохраняется. Появление нелинейности в исходной кривой тут же приводит к возрастанию погрешности аппроксимации. Совершенно очевидно, что при наложении на кривые случайных возмущений немедленно вызовет рост погрешности. В соответствии с этим будем строить линейную (в смысле линейных дифференциальных уравнений представления информационных, финансовых и материальных потоков) модель реальной системы. Или другими словами аппроксимировать реальные процессы отрезками, так называемых логистических кривых – результат хорошо известный в экспериментальном анализе экономических процессов. Прибыль предприятия до налогообложения представляет собой разность между выручкой (нетто) и себестоимостью оказанных услуг. Тем самым соответствующий график позволит нам, в определенной степени судить о точности верификации модели.

Рис. 3.11. Подгонка параметров модели по переменной себестоимость

Сделанное нами заключение о возможности представления реальной системы линейной имитационной моделью позволяет существенно упростить вероятностный анализ имитационной модели.

А именно, уравнения для математических ожиданий – уравнения имитационной модели, в которых все случайные составляющие приняты равными нулю, если использовать матричную форму записи уравнений имитационной модели. В предельном случае разностное уравнение заменяется соответствующим дифференциальным уравнением.

Рис.3.12. Моделирование прибыли при проверке точности аппроксимации модели реальной системе.

Обозначим:

– вектор переменных имитационной модели. n – число переменных модели.

Квадратная матрица размером темпов увеличения и уменьшения. Явный вид этой матрицы мы не приводим, вследствие ее громоздкости и проведения всех расчетов на ПК.

– вектор нормальных взаимно независимых белых шумов.

Тогда уравнения имитационной модели в векторном виде будут иметь вид:

Или в спектральном представлении (см. А.Корн “Справочник по математике для научных работников и инженеров”:

,

решение этого уравнения хорошо известно:

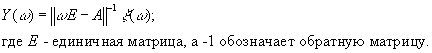
Обозначая чертой сверху соответствующие математические ожидания для их определения имеем однородное дифференциальное уравнение:

Аналитическое решение которого получается путем определения собственных чисел матрицы .

По причинам, описанным выше мы не приводим аналитической зависимости для корреляционных моментов исследуемых процессов. Для определения оценок дисперсий исследуемых процессов использовался метод Монте-Карло.

Программа имитационного моделирования была написана на языке Дельфи 6. Случайные процессы моделировались при помощи стандартной функции Randomize.

Начальный момент интегрирования положим равным , шаг интегрирования полгода. Если временную шкалу измерять в годах, тогда , а момент окончания интегрирования будет равен . Для определенности примем, что время выполнения услуги равно 0, 25 (одному кварталу).

Введем обозначения:

Количество услуг ® y[1]

Количество клиентов ® y[2]

Количество менеджеров ® y[3]

Количество случаев обслуживания ® y[4]

Себестоимость ® Y[5]

Доход ® y[6]

Стоимость вспомогательного оборудования ® Y[7]

Прибыль ® y[8].

Используя результаты подгонки параметров модели имеем начальные условия:

В соответствии с прайс-листом фирма “Русмар”, на момент начала прогноза, оказывала 6 услуг.

y[1] = 6.

У нее находилось на обслуживании 100 клиентов.

y[2] = 100.

Пусть ежегодно повышают квалификацию 20% менеджеров. В начальный момент в отделе маркетинга работало 10 менеджеров, из них два человека квалифицированные.

 Скачать реферат