Характеристика систем складирования и размещения запасов

Оптимальным будет то число укрупненных бригад грузчиков и рабочих, при котором сумма затрат по простою автомобилей и бригад минимальна.

Не приводя вычислений, напишем выражение, характеризующее вероятность того, что все обслуживающие аппараты заняты:

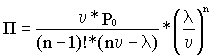, (8.20)

откуда среднее время ожидания начала обработки из-за занятости укрупненных комплексных бригад равно:

, (8.21)

а простой автомобилей в единицу времени вследствие отсутствия свободных укрупненных комплексных бригад

, (8.22)

Математическое ожидание числа простаивающих бригад (среднее число свободных обслуживающих аппаратов):

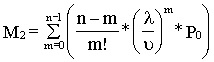, (8.23)

где Р0 – вероятность, что все обслуживающие аппараты (комплексные бригады) свободны и равны.

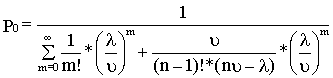, (8.24)

Потери (убытки) в сутки, вызванные простоем автомобилей, определяем в приведенных затратах:

Ra = Gож * Эф, (8.25)

где Эф – убытки в результате простоя автомобиля за час, руб.

В связи с простоем укрупненных бригад, обслуживающих базу, а с ними и расходы по базе, связанные с простоем бригады, определяем из

Rб = Эб * М2, (8.26)

где Эб – убытки часа простоя бригады; М2 – математическое ожидание числа простаивающих бригад в ожидании погрузки автомобилей.

Для производства соответствующих расчетов с помощью математического аппарата теории массового обслуживания необходимо определить значение параметров.

Параметр , характеризующий среднее число автомобилей, прибывающих на базу в течение рабочего дня, определяется по формуле:

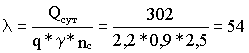(автомобиля),

где Qсут – суточный грузооборот, т; nс – количество ездок автомобилей; – коэффициент использования грузоподъемности; q – грузоподъемность автомобиля, т.

Чтобы определить значение параметра , необходимо предварительно рассчитать средний простой автомобилей под погрузкой tпр под грузовыми и вспомогательными операциями.

Время простоя под грузовыми операциями автомобиля определяем из уравнения:

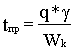, (8.27)

где tпр – продолжительность нахождения автомобиля под погрузкой, ч; W – производительность комплексной бригады.

Таблица 4

Время простоя автомобиля и значение параметра и в зависимости от производительности комплексной бригады

Зная параметры  и , определяем число бригад, принимая во внимание, что производительность в час равна 40 т, из соотношения /. Поскольку / = 54/18 = 3, то минимальное число бригад будет равно четырем.

Таким образом, рассмотрим транспортный процесс с четырьмя бригадами. Начнем с вычисления вероятности того, что в момент прибытия автомобилей под погрузку обслуживающие бригады свободны (формула 8.24):

.

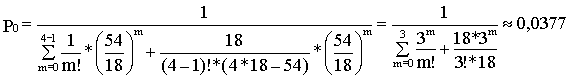Рассчитаем первое слагаемое:

=1+3+4,5+4,5=13.

Второе слагаемое:

,

откуда

.

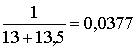Теперь вычислим вероятность того, что в момент прибытия очередного автомобиля под погрузку все комплексные бригады заняты (формула 8.20):

.

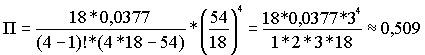Среднее время ожидания одним автомобилем начала погрузки вследствие занятости бригад определяем по формуле (8.21):

.

Поскольку среднесуточное количество автомобилей, прибывающих на базу под погрузку, составляет 54, то простой автомобилей за смену в ожидании погрузки составит:

= Gож *  = 0,028 * 54 = 1,512 автомобиле-часов,

а потери (убытки) в сутки, вызванные простоем автомобилей, в приведенных затратах по формуле (8.25) равны:

Rа = – Эа= 1,512 * 0,412 = 0,62 тыс. руб.,

где Эа – убытки простоя автомобиля за час, тыс. руб.

Определим математическое ожидание числа простаивающих бригад в ожидании погрузки автомобилей при m = 4 по формуле (8.23):

.

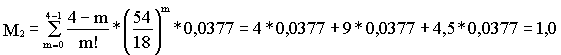Следовательно, в сутки будет простаивать одна бригада, а расходы предприятия, связанные с простоем бригады, по формуле (8.26) составят:

Rб = M2 * Эб = 1 * 3,0 = 3,0 тыс. руб./ч,

где Эб – убытки часа простоя бригады, равные 3 тыс. руб.

Произведенные расчеты показывают, что убытки по предприятию, вызванные простоем автомобилей и простоем бригад, составят:

R = Ra + Rб = 0,62 +3,0 = 3,62 тыс. руб./ч.

Данные аналогичных расчетов вариантов с пятью и шестью комплексными бригадами приведены в табл. 5.

Таблица 5

Из приведенных расчетов видно, что оптимальным вариантом является загрузка автомобилей четырьмя бригадами. Следовательно, оптимальная численность транспортно-складских рабочих составит 16 человек (4х4).

Отсутствие грузчиков, в равной мере как и отсутствие погрузочно-разгрузочных механизмов, влияет на использование производительности подвижного состава, приводит к большим простоям, отсюда ведет к убыткам транспортной организации и к увеличению количественного состава автомобилей. Поэтому определение оптимального количества транспортно-складских рабочих имеет большое значение для фирм, транспортных и сбытовых организаций. Мы рассмотрели только некоторые вопросы грузовой и коммерческой работы. Однако их решение позволит повысить эффективность продвижения материалопотока, улучшить взаимодействие снабженческо-сбытовых и автотранспортных организаций, а также использование машин и механизмов, повысить прибыль на предприятиях оптовой торговли.

 Скачать реферат