Метод экспертных оценок

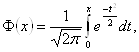
для которой имеются таблицы [7]. После вычисления порогового значения оценка коэффициента корреляции считается значимой, если .

Для определения значимости оценки коэффициента Спирмена можно воспользоваться критерием Стьюдента, поскольку величина [12]

(5.61)

приближенно распределена по закону Стьюдента с n – 2 степенями свободы.

Если в ранжировках имеются связанные ранги, то коэффициент Спирмена вычисляется по следующей фор­муле [12]:

(5.62)

где - оценка коэффициента ранговой корреляции Спирмена, вычисляемая по формуле (5.59), а величины равны [12]

(5.63)

В этих формулах и - количество различных связан­ных рангов в первой и второй ранжировках соответст­венно.

Коэффициент ранговой корреляции Кендалла при от­сутствии связанных рангов определяется формулой [12]:

где n – количество объектов, - ранги объектов, sign x – функция, равная [12]

sign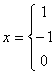

Сравнительная оценка коэффициентов ранговой кор­реляции Спирмена и Кендалла показывает, что вычис­ление коэффициентов Спирмена производится по более простой формуле. Кроме того, коэффициент Спирмена дает более точный результат, поскольку он является оп­тимальной по критерию минимума средней квадрата ошибки оценкой коэффициента корреляции.

Отсюда следует, что при практических расчетах кор­реляционной зависимости ранжировок предпочтитель­нее использовать коэффициент ранговой корреляции Спирмена.

ЗАКЛЮЧЕНИЕ

Динамизм и новизна современных народнохозяйственных задач, возможность возникновения разнообразных факторов, влияющих на эффективность решений, требуют, чтобы эти решения принимались быстро и в то же время были хорошо обоснованы. Опыт, интуиция, чувство перспективы в сочетании с информацией помогают специалистам точнее выбирать наиболее важные цели и направления развития, находить наилучшие варианты решения сложных научно-технических и социально-экономических задач в условиях, когда нет информации о решении аналогичных проблем в прошлом.

Использование метода экспертных оценок помогает формализовать процедуры сбора, обобщения и анализа мнений специалистов с целью преобразования их в форму, наиболее удобную для принятия обоснованного решения.

Но, следует заметить, что метод экспертных оценок не может заменить ни административных, ни плановых решений, он лишь позволяет пополнить информацию, необходимую для подготовки и принятия таких решений. Широкое использование экспертных оценок правомерно только там, где для анализа будущего невозможно применить более точные методы.

Экспертные методы непрерывно развиваются и совершенствуются. Основные направления этого развития определяются рядом факторов, в числе которых можно указать на стремление расширить области применения, повысить степень использования математических методов и электронно-вычислительной техники, а также изыскать пути устранения выявляющихся недостатков.

Несмотря на успехи, достигнутые в последние годы в разработке и практическом использовании метода экспертных оценок, имеется ряд проблем и задач, требующих дальнейших методологических исследований и практической проверки. Необходимо совершенствовать систему отбора экспертов, повышение надежности характеристик группового мнения, разработку методов проверки обоснованности оценок, исследование скрытых причин, снижающих достоверность экспертных оценок.

Однако, уже и сегодня экспертные оценки в сочетании с другими математико-статистическими методами являются важным инструментом совершенствования управления на всех уровнях.

 Скачать реферат